abc is dilated about the origin. what scale factor was used to make the image abc?
Dilation
In mathematics, dilation is a type of transformation in which the size of a shape or geometric figure is inverse, only the relative proportions and shape remain the same. Beneath are several examples.
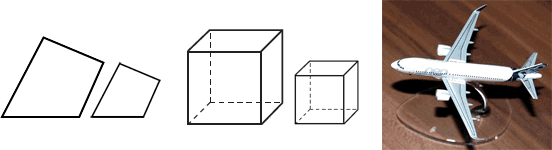
The quadrilateral and cube higher up are dilated to produce smaller versions of the corresponding shapes. The model airplane to the right is dilated to i-thousandth the size of the real plane.
The term "preimage" is used to refer to a geometric figure earlier it has been transformed and the term "image" is used afterwards it has been transformed. Dilation is a not-rigid transformation, which means that the distance betwixt points in the preimage and image don't remain the same; the preimage and epitome are not congruent. Dilation can refer to either an increment or a decrease in size.
Scale cistron
A scale factor is a number past which a quantity is multiplied, changing the magnitude of the quantity. In the context of dilation, the scale factor is the value that determines both whether the preimage increases or decreases in size, as well as the magnitude of the modify with respect to a stock-still point chosen the center of dilation. A center of dilation can either be function of the preimage or outside of the preimage. Below are some examples of both cases.
Scale factor between 0 and one.
If the calibration cistron is betwixt 0 and 1, the preimage decreases in size.
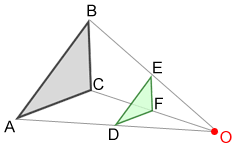
△ABC~△DEF
The preimage of triangle ABC is dilated with respect to indicate O by a scale factor of to produce the prototype of triangle DEF. The length of each side of the preimage is multiplied by
to produce each respective side of the image. Also, points on triangle DEF are
the distance from O relative to their corresponding points on triangle ABC.
Scale factor greater than 1
If the scale factor is greater than 1, the preimage increases in size.
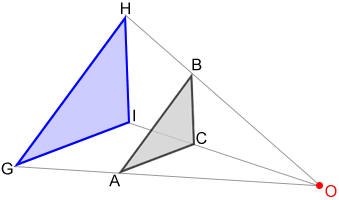
△ABC~△GHI
Triangle ABC is dilated with respect to point O past a scale factor of to produce triangle GHI. The length of each side of the preimage is multiplied past
to produce each corresponding side of the epitome. As well, points on triangle GHI are
the distance from O relative to their respective points on triangle ABC.
Where does the prototype "land"?
When the scale factor is between 0 and 1, the image is between the preimage and the center of dilation. When the scale factor is greater than 1, the preimage is between the image and the center of dilation.
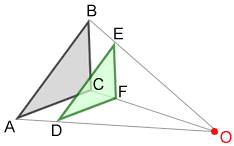
Beneath is a diagram showing a composite of the ii dilations of triangle ABC.
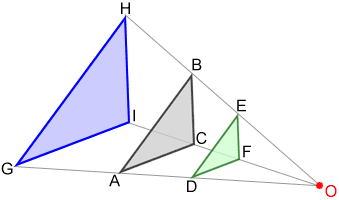
△ABC~△DEF~△GHI
Triangle DEF lies between the preimage of triangle ABC and point O, the center of dilation, since the scale factor was less than 1. Triangle ABC lies between the dilated triangle GHI and the heart of dilation since the calibration cistron was greater than i. Also, all three triangles are similar.
The closer the scale factor is to one, the closer the image of the dilated triangle is to the preimage. Triangle ABC is dilated by a scale factor of to produce triangle DEF:
How to determine the scale cistron
The scale factor tin can be determined by taking the ratio of the distance between a point on the image and the center of dilation to the altitude between a corresponding signal on the preimage and the center of dilation.
Example:
Find the scale gene if quadrilateral ABCD is dilated to produce quadrilateral EFGH for the middle of dilation O below.
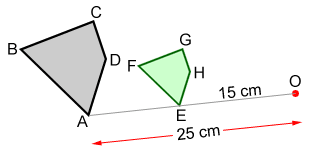
This means that the lengths of the sides of quadrilateral EFGH are the lengths of the corresponding sides of quadrilateral ABCD; conversely ABCD is
the size of EFGH.
Dilations in coordinate geometry
In a second coordinate airplane, a dilation with origin as the dilation eye and a scale factor of "a" volition maps a bespeak (x, y) to (ax, ay). The following are some examples.
Heart of dilation outside of the geometric figure
Triangle ABC is dilated by a factor of 0.5 to produce triangle DEF. The coordinates of the vertices of triangle ABC are A (2, vi), B (4, 6), and C (4, 2). Dilating triangle ABC by a factor of 0.v results in triangle DEF with vertices D (1, 3), Due east (2, 3), and F (2, 1).
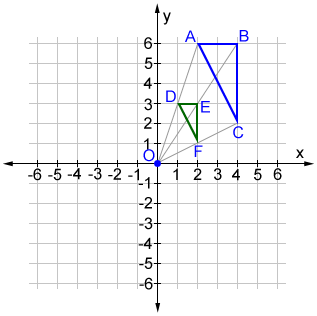
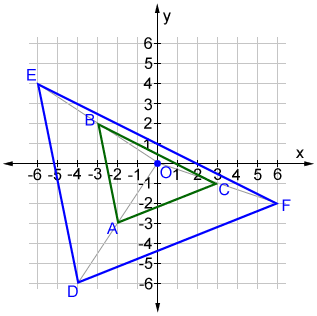
Center of dilation inside of the geometric figure
Triangle ABC is dilated past a factor of ii to produce triangle DEF. The coordinates of the vertices of triangle ABC are A (-2, -3), B (-3, ii), and C (3, -i). Dilating triangle ABC by a cistron of two results in triangle DEF with vertices D (-iv, -6), E (-half-dozen, 4) and F (half-dozen, -2).
Negative calibration factors
When the scale factor is negative, the origin lies betwixt the preimage and the image. The size of the epitome is the same equally it is when the scale cistron is positive, simply is graphed in the opposite management.
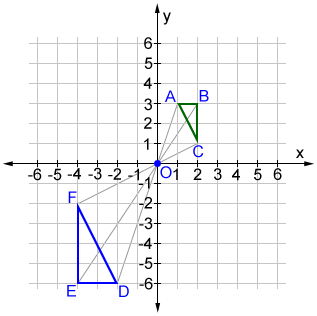
Triangle ABC is dilated by a scale factor of -2 to produce triangle DEF. The coordinates of the vertices of triangle ABC are A (one, 3), B (2, 3) and C (2, 1). Dilating triangle ABC past a scale factor of -ii results in triangle DEF with vertices D (-ii, -6), E (-4, -6), and F (-4, -2).
Center of dilation is not the origin
Let (c, d) be the coordinates of the center of dilation. Given that a is a calibration factor that is greater than zero, the bespeak (x, y) is dilated to a point (10', y'), as shown below.
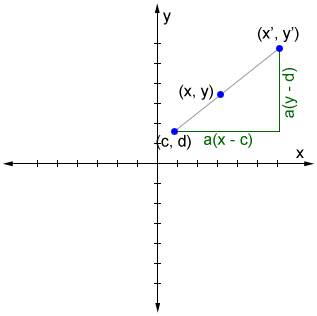
To decide the coordinates of the dilated bespeak, add the horizontal and vertical distances to the x- and y-coordinates of the eye of dilation:
(x', y') = (c + a(10 - c), d + a(y - d))
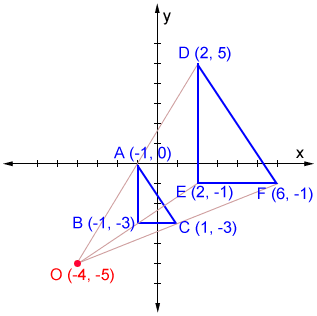
Example:
Dilate triangle ABC given vertices A (-one, 0), B (-i, 3), and C (1, -three), calibration cistron of 2, and a eye of dilation of O (-4, -5).
Using the formula from above, we tin find the coordinates for the new vertices D, Due east, and F and graph them equally follows:
| D = | (-four+ii(-1-(-four)), -5+2(0-(-five))) |
| = | (2, 5) |
| E = | (-four+two(-i-(-4)), -v+2(-3-(-5))) |
| = | (two, -1) |
| F = | (-4+two(1-(-4)), -5+2(-3-(-5))) |
| = | (vi, -1) |
Source: https://www.math.net/dilation
0 Response to "abc is dilated about the origin. what scale factor was used to make the image abc?"
Post a Comment